邱健蓄电池提出的平整度电磁体系

1 提出的平整度电磁体系

所提出的依据平整度操控理论的高效能量办理体系提供了一种高效率、鲁棒性和非线性的能量办理战略，与依据经典线性PI的能量办理体系比较。该战略旨在最小化等效发电能耗，并在所有负载或气候条件下延伸体系单元（如光伏体系、燃料电池、超级电容器和锂离子电池）的运用寿命。所提出的战略经过体系的各种参数进行运用，如直流负载需求、发电量、锂离子电池和超级电容器的SOC。

1.1 非线性平面度理论

非线性体系的操控电路规划或许比线性体系更杂乱，因为非线性体系存在非线性问题，而线性体系在操控电路的规划和实现上较为简单。因而，运用微分平整性理论到非线性体系中，以下降和简化模型的阶数。因而，替代模型答应依据[42]对轨迹的动态进行描述。因而，经过运用该理论，可以以为非线性体系是平整的。以下方程可以表明这个平整模型：

    其间 \( y \) 是平整度模型的输出，\( \chi \) 是状态变量，\( u \) 是操控变量。此外，\( \phi \)、\( \varphi \) 和 \( \psi \) 是平滑映射的函数，而 \( y^{(\beta+1)} \) 是输出 \( y^{(\beta+1)} \) 的导数符号。另外，\( \alpha \) 是导数的有限数，一起 rank = m、rank = n 和 rank = p [18]。

1.2 体系装备计划

 本研讨中运用的光伏、燃料电池、超级电容和电池体系的建议能量办理体系及直流/直流电源转化器如图2所示。光伏体系经过一个升压变换器电路进行操控和接口，以依据粒子群优化（PSO）的最大功率点盯梢（MPPT）操控器实现最大功率点盯梢算法。在这里运用直流/直流两相交织升压变换器的目的是盯梢光伏体系的最大功率点，并使光伏和燃料电池体系的输出电压在直流母线侧等于380伏。超级电容和锂离子电池由两个相并联的双向变换器操控。本作业中运用的直流微网组件的尺寸或额定值列在表1中。

 

所提出微电网体系中运用的组件尺寸

组件	值
光伏体系标准	3000瓦，170伏
FC标准	6000瓦，45伏
超级电容器的容量	100℉，48伏
电池容量	600安时，48伏

Fig. 2:

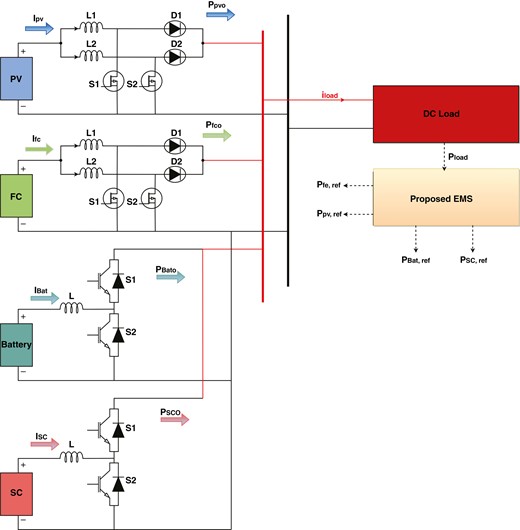
体系装备计划。

1.3 两相升压变换器规划

运用这种变换器的首要目的是与传统升压变换器比较，减小电流纹波和开关损耗。两相升压变换器是经过将两个升压电路并联衔接，然后将驱动信号移相180度来实现的。两相交织升压变换器可以依据以下方程规划，这些方程是在接连导通方法下推导出来的，而且坚持占空比小于依据电感电流关键波形的占空比，如图3所示。因而，电感电流的上升斜率可以如下给出：

Fig. 3:

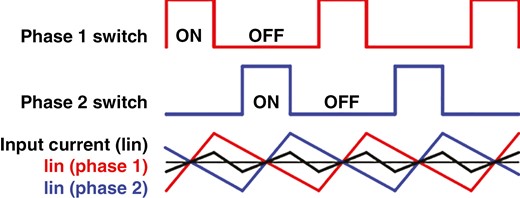
两相升压变换器电路在接连导通方法下的关键波形。

   
(4)

   其间 \(V_{in}\) 是两相升压变换器的输入电压，等于 \(V_{PV}\)，\(V_{out}\) 是升压变换器的输出电压，\(L_{in}\) 是输入电感器。为了核算所需电感值，有必要依照以下方法核算输入电流的峰峰值纹波[43]：

  
(5)

其间 \( T \) 是总周期时间，记作 \( T = \frac{1}{f_{sw}} \)，其间 \( f_{sw} \) 表明约为 5 kHz 的开关频率。两相升压变换器的输出电压与输入电压之比可以写成 [43]：

 
(6)

 此外，经过将方程（6）中的Vin代入，可以得到d<0.5时的输入电流纹波：

  
(7)

其间 \( I_{in} \) 是输入电流，\( \Delta I_{in} \) 是输入电流的改变量。为了进一步简化，输入电感值可以从以下方程中核算[43]：

    
(8)

  注意，输入电感值有必要较大，以避免断续导通方法。因而，两相电感值挑选为 \( L_{in} = 1 \) mH。占空比等于 \( d = 0.45 \)，而且 \( \Delta I_{in} = 0.3 I_{in} \)。

1.4 双向转化器规划

 超级电容器和锂离子电池的充放电过程经过双向直流/直流变换器进行操控。该变换器经过运用小电感值来减小输入电流纹波，然后改善开关操作[32]。因而，转化阶段的效率得到了进步，ESS的动态性和安全性也得到了进步。flatness EMS经过操控这些变换器的输出电流并将其与参阅值（ISC,ref,IB,ref）进行比较，为这些变换器生成适当的占空比周期来操控超级电容器和电池。此外，依据两种作业方法（降压方法和升压方法），可以对两个相的双向变换器进行剖析，如[44]所示。假如变换器在降压方法条件下作业，则输入电池或超级电容电压（Vin）被施加到电感器上，电感可以如下核算：

 
(9)

 其间 \(\Delta i_L\) 表明电感电流的改变。在这种状况下，占空比将在所需的直流母线电压值的基础上从 \(d_{min}\) 改变到 \(d_{max}\)，其间 \(d_{min}\) 和 \(d_{max}\) 分别是最小和最大占空比。这种变换器的操控使直流母线电压坚持在参阅值恒定。此外，假如变换器以升压方法运行，直流母线电压 \(V_{dc,Link}\) 和输入电压之间的联系将是：

(10)

在这种状况下，输入电感器可以依据以下方程[44]核算：

      
(11)

1.5 提出模型的运用平整度

  在本文中，要操控的首要三个变量是直流母线能量、超级电容能量和电池能量。光伏、燃料电池、超级电容和锂离子电池电源的源和储能体系的内部操控环可以作为一个增益统一研讨。光伏体系(PPV,ref)、燃料电池体系(PFC,ref)、超级电容(PSC,ref)和锂离子电池(PB,ref)的参阅功率经过水平 EMS 操控，这些变量可以写成：

 

    其间，\( v_{PV} \) 和 \( i_{PV} \) 是光伏体系的电压和电流瞬时值，\( v_{FC} \) 和 \( i_{FC} \) 是燃料电池体系的电压和电流瞬时值，\( v_{B} \) 和 \( i_{B} \) 是电池的电压和电流瞬时值，\( v_{SC} \) 和 \( i_{SC} \) 是超级电容器的电压和电流瞬时值。

此外，直流母线电容能量 \( y_{\text{bus}} \) 和超级电容器能量 \( y_{\text{SC}} \) 可以表明如下[18]：

 

其间Cbus是直流母线的电容，vbus是瞬时电压母线，CSC是超级电容的电容。

然而，为了保证所提出电厂的EMS高效运行，直流母线电容能量的导数电容能量 \( y_{bus} \) 以差分方程的方法表明，相对于光伏体系的实际输出功率、FC、SC、电池和直流负载如下[18, 32]：

(18)

实际输出功率，包括其电路中的转化器静态损耗，可以写成以下方程：

其间 \( r_{PV} \)、\( r_{FC} \)、\( r_B \) 和 \( r_{SC} \) 分别是光伏、燃料电池、电池和超级电容器的转化器丢失。

依据前文剖析的成果，超级电容设备为了实现直流母线安稳，会向需求负载提供最快速可用的能量。在多种不同状况下运行时，锂离子电池会被用来给超级电容充电。电池将会由光伏和燃料电池等可再生动力进行充电，这些动力一起也作为主发电机运用。此外，电池将在参阅条件下进行维护。为了下降模型的阶数并展示所建议的平整化能量办理体系，平整化操控被运用于所提出的电力体系。依据前文所述，所建议的模型将被界说如下[18]：

    
(24)

经过将这一理论运用于所提出的体系，界说了以下方程：

    
(25)

1.6 直流母线电压操控

  为了操控直流母线电压，平整的输出 \( y_1 \)，直流母线的状态变量 \( x_1 \) 和输入操控单元 \( u_1 \)：

  
(26)

输入操控变量可以从方程(18-23)中推导出来，并可以写成如下方法[18, 32]：

    
(27)

其间SC的最大功率由 \(P_{\text{SC},\text{max}} = \frac{\upsilon_{\text{sc}}^2}{4r_{\text{sc}}}\) 给出。

操控方针是调理直流母线的电压或母线电容能量，即 \( y_{\text{bus}} = y_1 \)。因而，运用 PI 操控器来安稳和调理直流母线电压。实际上，考虑到超级电容操控环比电池和燃料电池快，所以方程（18）中提出的模型的总功率可以写成：

(28)

从这个方程式中可以清楚地看出，输出传递函数是一个纯积分器。因而，在本研讨中，依据假定 \( y_{ref} = y_{bus,ref} \)，采用了一个PI操控器，而且为了保持低直流母线电压的操控方程表明为[18, 32]中的样子：

 
(29)

    其间 \( K_p = 2 \cdot \zeta \cdot \omega_n \)，\( K_i = \omega_n^2 \)，\( \omega_n \) 是固有频率，\( \zeta \) 是阻尼因子。

为了运用Li-ion电池设备给超级电容器充电，方程（18）有必要重写为方程（30）的方法，忽略丢失，并设置 ybus=常数：

     
(30)

此外，运用PI操控器来创立SC的需求功率，然后将其作为参阅功率项[18]以如下方法提供给电池：

      
(31)

  其间 \( v_{SC} \) 是超级电容器的电压参阅值，\( K_1 \) 是超级电容充电操控的增益比例，\( K_2 \) 是超级电容充电操控的积分增益。

图4显示了超级电容器的充电状况以及直流母线电压安稳性的操控状况。

Fig. 4:

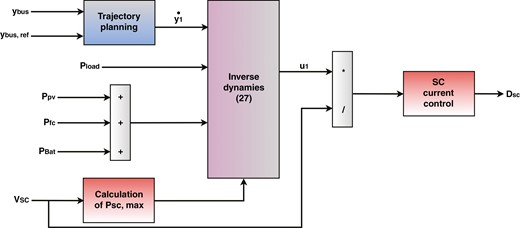
运用平整度操控理论的直流母线电压操控。

1.7 锂离子电池的充电和操控

为了使光伏和燃料电池可以为锂离子电池充电，方程(18)应该改写如下：

     

电池能量办理体系用于监测超级电容器的电压，如图5所示。电池所需的功率经过超级电容器的需求功率来近似核算，这是为了实现所需功率而进行的。此外，还增加了电池电流操控，以调理电池的充电和放电值。在这种装备中，用于给电池充电的电流具有负值，而用于放电的电流具有正值。此外，这些电流被发送到操控单元，以延伸锂离子电池的运用寿命并保证电池可以继续更长时间。因而，经过运用一阶滤波器，电池的功率动态发生了改变，如下面的方程[32]所示：

Fig. 5:

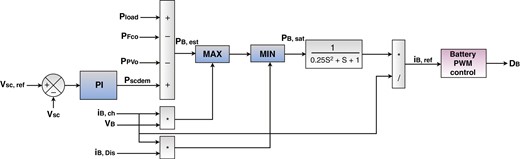
所提出的能量办理体系和电池操控，其间PWM代表脉冲宽度调制。